Introduction
Si vous êtes familier avec le machine learning (ML) il est fort probable que la question de l’explicabilité ou de l’interpretabilité d’un modèle ne vous soit pas étrangère. En effet, créer un modèle de ML pour prédire est une chose, comprendre comment, sur quelles décisions le modèle prédit, en est un autre.
Selon Miller (2017) l’interprétabilité est, je cite:
la faculté grâce à laquelle un être humain peut comprendre la cause d’une décision.
Dès lors, appliquer la définition de Miller au ML consiste à caractériser l’interpretabilité d’un modèle comme niveau de compréhension qu’un individu peut avoir dans sa prédiction.
Expliquer, à quelle finalité ?
Un modèle peu voire pas du tout explicable est catégorisé comme étant une boîte noire (Black box) et inversement, un modèle explicable est appelé une boîte blanche (White box). À choisir entre une boîte noire et une boîte blanche, notre dévolu se porterait sur cette dernière dans la mesure où comprendre les prédictions permettrait a posteriori d’ajuster au mieux nos propres décisions. Pour étayer mes propos je vais utiliser le secteur immobilier. Imaginez que l’on veuille prédire le prix d’un appartement sur Paris. Il serait intéressant de savoir quelles sont les variables/features contribuant le plus à la prédiction. De même, connaitre dans quelle mesure la prédiction varie en fonction de l’arrondissement serait une information intéressante (Ex: un appartement dans le 16e sera prédit plus cher qu’un appartement dans le 20e par exemple).
L’exemple que j’ai choisi est relativement basique, mais il se pourrait que dans certaines situations les informations issues de l’explicabilité du modèle soient essentielles, voire obligatoires. En effet, imaginez un conseiller immobilier faisant une estimation de bien en s’appuyant sur la décision d’un modèle, il devrait être capable de justifier aux propriétaires les raisons de cette estimation sans quoi cette dernière pourrait s’avérer infondé.
En allant plus loin, l’exemple que nous venons de développer nous amène à prendre en considération les aspects légaux de l’explicabilité. Ainsi, l’article 22 du RGPD prévoit des dispositions visant à protéger les êtres humains contre des décisions prises exclusivement par des machines:
La personne concernée a le droit de ne pas faire l’objet d’une décision fondée exclusivement sur un traitement automatisé, y compris le profilage, produisant des effets juridiques la concernant ou l’affectant de manière significative de façon similaire. Dès lors, les modèles sans explication risquent d’entraîner une sanction qui peut s’élever à 20 000 000€ ou, dans le cas d’une entreprise, à 4% du chiffre d’affaires mondial total de l’exercice fiscale précédent.
Je pense que vous comprenez désormais l’importance de l’explicabilité de modèle en ML et les enjeux associés. Dans la partie suivante nous allons justement voir comment interpréter un modèle avec la librairie SHAP!
SHAP (SHapley Additive exPlanations)
Qu’est ce que c’est ?
Développé par Lundberg and Lee (2016), SHAP est une librairie permettant d’expliquer chacune des prédictions d’un modèle. SHAP s’appuie sur la théorie des jeux en utilisant le concept de valeur de Shapley.
L’idée est la suivante, pour chaque feature de chaque exemple du dataset vont être calculées les valeurs de Shapley :
Avec M, le nombre de variables, S est un sous-ensemble de variables, x est le vecteur des valeurs des features de l’exemple à expliquer. f(x) est la prédiction utilisant les valeurs des features dans l’ensemble S qui sont marginalisées par rapport aux features qui ne sont pas inclues dans l’ensemble S (Si la formule n’est pas claire, pas de soucis, nous detaillerons le calcul de la valeur de Shapley dans la section suivante)
L’une des propriété de SHAP est l’additivité. Cela signifie que chacune des prédictions pour chaque observation peut s’écrire comme la somme des valeurs de shapley ajoutée à la prédiction moyenne notée (valeur de base)(Voir Fig.1):
Avec, y_pred la valeur prédite du modèle pour cet exemple, la valeur de base du modèle,
quand la variable est observée
=1 ou inconnue
=0.
Figure 1: Additivité des valeurs de shapley (La somme des valeurs de shapley ajoutée à la valeur de base est égale à la prédiction)
Pour finir cette partie, quoi de mieux qu’un exemple pour illustrer ! Pour cela, reprenons notre example fétiche. Imaginez un appartement dont la valeur est prédite à 530 000 €. L’appartement à une superficie de 75m², possède un balcon et est situé dans le 16e arrondissement (dans la réalité l’appartement serait bien plus cher…). Par ailleurs, le prix moyen d’un logement sur Paris est de 500 000€. Notre appartement est donc 30 000€ plus cher que le prix moyen prédit. L’objectif est donc d’expliquer cette différence. Dans notre exemple, il est probable que la superficie contribue à hauteur de 15 000€, la présence d’un balcon de 5 000€ et l’arrondissement à 10 000€. Ces valeurs sont les valeurs de shapley.(Note: Dans le cadre d’une classification les valeurs de shapley augmentent/diminuent la probabilité moyenne prédite).
Comment calculer une valeur de shapley ?
S’il fallait retenir une chose, ca serait la suivante: La valeur de shapley est la contribution marginale moyenne de la valeur d’un feature au travers de toutes les coalitions possibles.
Pour comprendre cette définition nous allons chercher à évaluer la contribution de l’arrondissement lorsqu’elle est ajoutée à la coalition (combinaison de features) superficie - balcon. Dans l’exemple précedent nous avions prédit le prix d’un appartement en considérant sa superficie, la présence d’un balcon ou non et son arrondissement (16ème). Nous avons prédit un prix de 530 000€. Si on enlève arrondissement de la coalition en remplaçant la valeur ‘16eme’ par une valeur aléatoire de ce même feature (par exemple 13ème), on prédit un prix de 490 000€. L’arrondissement du 16eme contribue donc à hauteur de 40 000€ (530 000€ - 490 000€). Ainsi nous venons donc de calculer la contribution d’une valeur d’un feature (16ème) dans une seule coalition. Maintenant l’opération doit etre répétée pour toutes les combinaisons de coalitions possibles afin de déterminer la contribution marginale moyenne.
En conclusion, on calcule pour chaque coalition le prix de l’appartement avec et sans la valeur ‘16eme’ du feature arrondissement pour determiner la moyenne des différences (contribution marginale moyenne) dans toutes les coalitions.
SHAP en exemple
Maintenant que nous sommes familiers avec SHAP et les valeurs de shapley, nous allons pouvoir étudier un cas concret d’explicabilité de modèle. L’exemple que nous allons prendre s’appuie sur le dataset Health Insurance Cross Sell Prediction.
Descriptif
L’objectif via ce jeu de données est de déterminer si les clients d’une compagnie d’assurance seraient potentiellement intéressés pour souscrire à une assurance auto. Pour mener à bien cette tâche nous avons construit un modèle classifiant si oui ou non le client serait intéressé avec à notre disposition des informations relatives aux clients (Ex: genre, âge, sexe, région), l’état de leur véhicule (Ex: âge du véhicule,présence de dommages) et leur contrat d’assurance (Ex: somme versée par le client, moyen de contact du client). Bien entendu, nous cherchons à expliquer les prédictions du modèle (Ex: pourquoi ce client a été classifié comme susceptible de souscrire à l’assurance auto ?).
Dans cet article nous allons directement traiter de l’explicabilité avec SHAP. Si cela vous interesse, je vous invite à consulter le notebook complet ici avec les plots SHAP interactifs.
SHAP feature importance
Quand on parle de feature importance, on peut penser à plusieurs choses:
- Aux poids (weights) dans le cadre d’une régression linéaire. En effet, les variables ayant un poids élevé sont plus importantes dans le modèle (Notes: Uniquement si les variables sont à la même échelle).
- Le gain d’information (information gain) pour les modèles arborescents (les features qui réduisent davantage l’impurity sont plus importants).
SHAP peut être utilisé pour obtenir l’importance des features sur la base des valeurs de Shapley. Plus les features ont une moyenne de valeurs de Shapley (en valeur absolue) élevée, plus elles contribuent aux prédictions.
Figure 2: SHAP feature importance
En s’intéressant de plus près au feature importance plot (voir Fig.2), nous comprenons que les variables Previously_insured, Vehicle_damage et Policy_sales_channel sont les trois variables qui contribuent le plus aux prédictions.
(Notes: L’utilisation de l’importance de la caractéristique SHAP dans un cas de haute dimensionnalité pourrait être une bonne idée pour réduire la dimensionnalité en supprimant les caractéristiques ayant une faible moyenne des valeurs de Shapley).
SHAP summary plot
Le SHAP summary plot fournit des informations sur l’importance des features et leurs effets.
Chaque point du graphique est une valeur de Shapley pour chaque feature de chaque observation. La position est définie par la valeur de Shapley sur l’axe des x et les features sur l’axe des y. Sur la droite, la barre de couleur représente la valeur du feature, de faible (Bleu) à élevée (Rouge).
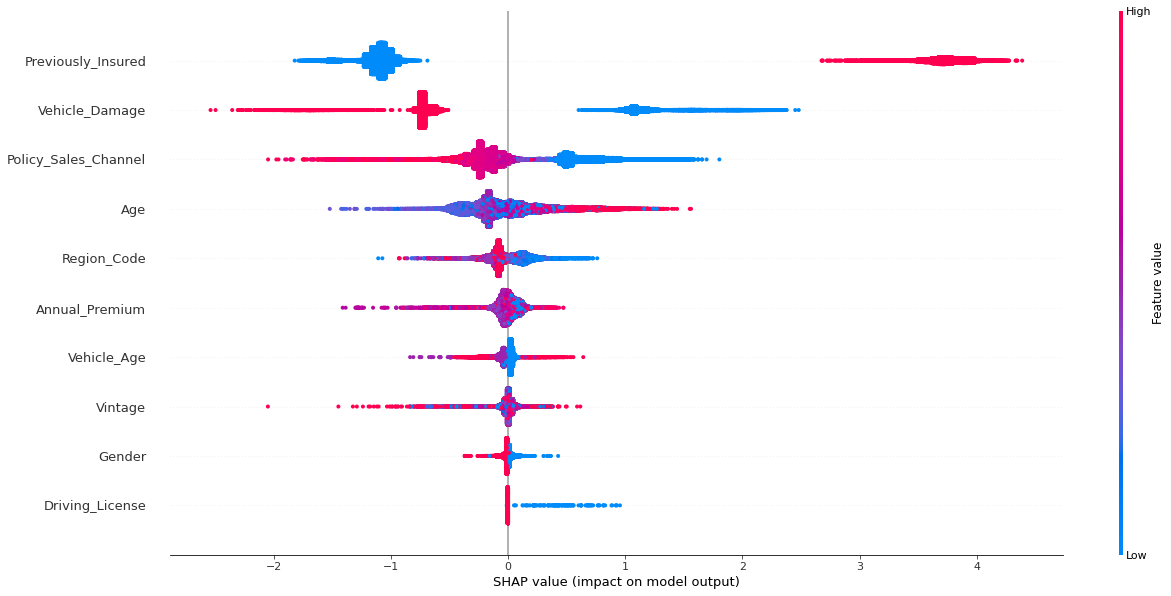Figure 3: SHAP summary plot
Ici, une faible valeur de Previously_insured (0 : non assuré) signifie une valeur SHAP négative qui diminue la probabilité d’être intéressé par une assurance automobile (Rappel: la prédiction est représentée comme la somme des valeurs SHAP). Au contraire, une valeur élevée de Previously_insured (1 : assuré) signifie une valeur SHAP positive qui augmente la probabilité d’être intéressé par une assurance automobile (Voir Fig.3).
Néanmoins, nous pouvons voir que certains effets sont difficiles à interpréter sur ce graphique car nous avons effectué une mise à l’échelle sur certaines variables. Pour une meilleure compréhension, il pourrait être utile d’explorer les effets au niveau individuel.
SHAP individual observation
Le force plot fournit par SHAP permet de comprendre les effets de chaque feature pour chaque observation. Nous allons voir directement comment cela se présente en étudiant le cas de deux clients.
Client 1
Figure 4: SHAP force plot client 1
Pour ce client (Voir Fig.4), nous constatons que le modèle prédit une probabilité de 0.61 qu’il soit interéssé par l’assurance et, par conséquent, qu’il soit classifié comme tel (1). En examinant le force plot, nous constatons que Age, Policy_Sales_Channel, Vehicule_Damage et Previously_Insured sont les principales variables qui augmentent la probabilité.
Comment cela peut-il être interprété ? Le fait que ce client soit âgé de 21 ans, qu’il ait déjà été assuré, que son véhicule n’ait pas été endommagé et qu’il ait été contacté par la chaîne en utilisant le code 152, augmente la probabilité (Rouge) d’être intéressé par une assurance automobile.
(Notes:Les valeurs continues sur le diagramme de force sont mises à l’échelle)
Client 2
Figure 5: SHAP force plot client 2
En ce qui concerne cet autre client (Voir Fig.5), le modèle prévoit une probabilité proche de zéro d’etre interéssé par l’assurance auto et est donc classé comme non intéressé (0).En effet, nous voyons que les effets des features les plus importants tendent à reduire la probabilité (Bleu).
Ce client n’ayant jamais été assuré auparavant, son véhicule n’ayant subi aucun dommage et ayant été contacté par un canal utilisant le code 26, cela réduit la probabilité d’être intéressé par l’assurance.
SHAP multiple observations
Si nous souhaitons examiner plusieurs observations, nous pouvons simplement superposer des force plots (dans l’exemple suivant, 1000 force plots ont été superposés). Les force plots sont pivotés verticalement et placés côte à côte en fonction de la similarité des effets des variables.
Figure 6: SHAP multiple force plot
Nous pouvons distinguer très clairement 2 types de cluster (voir Fig.6). Ces derniers ont été crées essentiellement par similarité des effets des features les plus importants, soit Previously_Insured, Vehciule_Damage et Policy_Sales_Channel :
- Les clients non intéressés (large portion bleue = réduit la probabilité).
- Les clients intéressés (large portion rouge = augmente la probabilité).
Figure 7: SHAP Age effect
Un force plot superposé peut également être utilisé pour observer l’effet de chaque feature. En prenant l’exemple de la variable Age (Voir Fig.7), nous déduisons qu’être âgé de 24 à 48 ans augmente la probabilité (Rouge), tandis que le fait de vieillir la réduit (Bleu) (Dans la mesure où nous avons utilisé l’age standard scalé pour le modèle, le plot utilise ces valeurs. Cependant il suffit simplement d’effectuer la transformation inverse pour obtenir l’age réel).
Conclusion
L’objectif de ce projet était de démontrer comment SHAP pouvait être utilisé pour expliquer les modèles de ML (dans notre cas, un modèle à arborescences = Tree-based model) et dans la continuité, apporter de nouvelles connaissances à forte valeur ajoutée. S’appuyant sur la théorie des jeux grâce aux valeurs de Shapley, SHAP dispose d’une base théorique solide, ce qui est en fait un atout considérable pour l’explicabilité.
En prenant un exemple dans le domaine de l’assurance, nous avons mis en évidence comment SHAP pouvait servir à calculer l’importance et les effets des features à échelle globale, mais aussi pour chaque observation d’un dataset.
En conclusion, SHAP peut être utilisé pour :
- Comprendre l’importance globale et locale des features
- Expliquer les prédictions d’un modèle de ML
- Comparer deux observations
- Créer des clusters d’observations par similarité des effets de variables